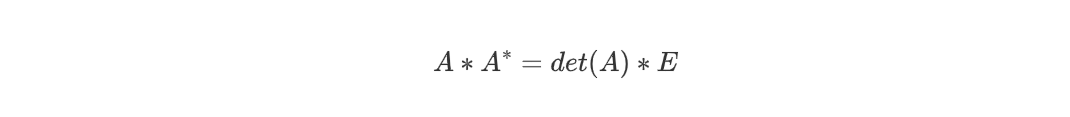Cybay
0%

矩阵求逆

发表于 更新于 分类于 Valine：
逆矩阵
相关公式

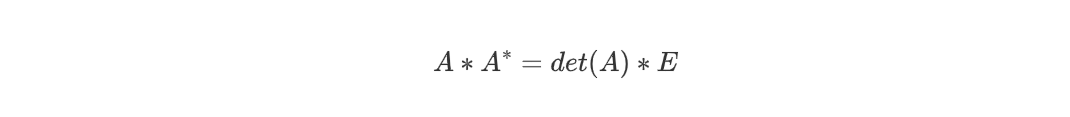
需求得矩阵A的行列式det(A)，求出A的伴随矩阵，每个元素除以det(A)即求得逆矩阵

求行列式

代码中计算n阶行列式的方式：用深度优先搜索算法获取n个不同行不同列元素的乘积，

用一个函数确定奇偶排列，将它们相加。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//判断奇偶排列
int serh(int a[])
{
    int cnt=0;
    for(int j=1;j<n;++j)
    {
        for(int i=j+1;i<=n;++i)
            if(a[j]>a[i])
                ++cnt;
    }
    if(cnt%2)
        return 0;
    return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//深度优先搜索
//k存放数的乘积，book数组
void dfs(int row,int k)
{
    if(row==n+1)
    {
        int temp=-1;
        if(serh(order))
            temp=1;
        sum+=temp*k;
        return;
    }
    for(int i=1;i<=n;++i)
    {
        if(book[i]==0)
        {
            order[row]=i;//更新顺序
            book[i]=1;
            dfs(row+1,k*a[row][i]);
            book[i]=0;//取消标记
        }
    }
    return;
}

总代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<iostream>
using namespace std;
int book[101],sum,n;
//行列式
int a[101][101],order[101];
int serh(int a[]);
void dfs(int row,int k);
int main()
{
    cin>>n;
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
            cin>>a[i][j];
    dfs(1,1);
    cout<<sum;
    return 0;
}

//深度优先搜索
void dfs(int row,int k)
{
    if(row==n+1)
    {
        int temp=-1;
        if(serh(order))
            temp=1;
        sum+=temp*k;
        return;
    }
    for(int i=1;i<=n;++i)
    {
        if(book[i]==0)
        {
            order[row]=i;
            book[i]=1;
            dfs(row+1,k*a[row][i]);
            book[i]=0;
        }
    }
    return;
}

//判断奇偶排列
int serh(int a[])
{
    int cnt=0;
    for(int j=1;j<n;++j)
    {
        for(int i=j+1;i<=n;++i)
            if(a[j]>a[i])
                ++cnt;
    }
    if(cnt%2)
        return 0;
    return 1;
}
求逆

可将求伴随矩阵与求逆的过程合并

遍历矩阵A，求出每个元素的代数余子式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//rac函数求行列式, 它的声明为
double rac(vector<vector<double> > a);


vector<vector<double> > a(n+1,vector<double>(n+1));//矩阵A

vector<vector<double> > rev(n+1,vector<double>(n+1));//存储逆矩阵

vector<vector<double> > rc(n,vector<double>(n));//A的子阵
	double xy;//系数


    for(int i=1;i<=n;++i){
        
        for(int j=1;j<=n;++j)
        {
            //上两层循环遍历A, 求a[i][j]的余子式
            
            int te1=1,te2=1;
            
            for(int k=1;k<=n;++k){
                
                for(int m=1;m<=n;++m)
                {
                    //下两层循环取得子阵
                    if(k!=i&&m!=j)
                    {
                        rc[te1][te2]=a[k][m];//存储子阵
                        te1++;
                        if(te1==n)
                        {
                            te2++;
                            te1=1;
                        }
                    }
                }
            }
            //求代数余子式
            if((j+i)%2)	 xy=-1.0;
            else  xy=1.0;
            
            //注意伴随矩阵以转置的顺序存储
            rev[j][i]=xy*rac(rc)/deta;
            
        }
    }
注意

最后，如果打印rev，如下

1
2
3
4
5
6
for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=n;++j)
            printf("%.2f ",rev[i][j]);
        putchar('\n');
    }

可能会打出-0.00，如图

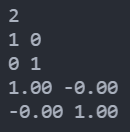
这是由于浮点数精度导致，0是不在浮点数表示范围内的

把打印语句改为

1
2
3
4
5
6
7
8
9
10
for(int i=1;i<=n;++i)
    {
        for(int j=1;j<=n;++j){
            if(rev[i][j]<=0&&(rev[i][j]+0.05>0)){
                printf("0.00 ");
            }
            printf("%.2f ",rev[i][j]);
        }
        putchar('\n');
    }

即可解决问题